A simple multi-agent experiment with random token exchange
03 Feb 2019
Hi! Thanks for visiting. Today I wanted to write about something that I had at the back of my mind since my undergraduate years.
On one of my physics lectures my professor presented us with a simple model backed up by a very simple game of randomly distributing things over a finite set of containers.
That was the most memorable and one of the fascinating things that captured my imagination and I would like to share it with you.
So without further ado let me introduce the problem.
Introduction
Let us have a set of N agents where each has a finite quantity of tokens. To make things initially simple let us start with thousand agents, i.e. N=1000 and initiate each one with 50 tokens:
\(B = \{b_{1}, b_{2},....b_{1000} \}\) where \(b_{k} = 50 \text{ for } 1<=k<=1000\).
Now let us define an simple exchange function \(E(b_{i}, b_{j})\) that will take a pair of agents \(b_{i} \text{ and } b_{j}\) where \(i \neq j\) and apply a random exchange from a set \(V \in \{-1, 0, 1\}\). \(V_{0}=-1\) dictates the direction of token exchange from \(b_{i}\) to \(b_{j}\), \(V_{1}=0\) means no exchange and finally \(V_{2}=1\) from \(b_{j}\) to \(b_{i}\). For now let’s prevent from agents ending up with less than zero tokens.
With the above simple initial conditions and definitions let’s ask some questions:
What would be the distribution look like after a very large number of such exchanges?What would be the proportion of buckets, say, with N >= 50 and N < 50?What would be the mean, standard deviation and what would be the closest analytical function describing the resulting distribution?
The coding experiment and implementation
To do the calculations I created a simple Python programme. The main function calls an AgentUniverse class shown in a code snippet below:
import random
import numpy as np
from .exchange_strategies import simple_exchange_strategy
import logging
import os
import json
log = logging.getLogger("agent_universe")
curr_dir = os.path.dirname(__file__)
class AgentUniverse:
#TODO need to generalise the way the universe can consume Agent class instead of dictionary
def __init__(self, agents, max_exchanges=100, total_agents=20, seed=42,
exchange_strategy=simple_exchange_strategy, output_data_filename=None):
"""Universe initializing an array of buckets
:param max_exchanges: Number of exchanges for universe to calculate
:param total_agents: number of existing agents
:param seed: Random seed for reproducibility
"""
self._max_exchanges = max_exchanges
self._total_agents = total_agents
self._exchange_strategy = simple_exchange_strategy
self._agents = agents
self.counter = 0
self._output_filename = output_data_filename
np.random.seed(seed)
if len(self._agents) <= 2:
raise ValueError("Number of agents can't be less than 2")
def _write_to_file(self):
if self._output_filename:
with open(file=self._output_filename, mode="a") as out_file:
log.info("Writing agent config after: {}".format(self.counter))
json.dump({"exchanges" : self.counter, "agents" : self._agents}, out_file)
def _select_pair(self):
"""Select a distinct pair of indexes for exchange from agent array """
i, j = np.random.choice(self._total_agents, 2)
if i != j:
return i, j
else:
return self._select_pair()
def _exchange_direction(self):
""" direction of exchange between buckets:
-1 i to j,
0 no exchange,
1 j to i
"""
return random.randint(-1, 1)
def _shuffle_and_exchange(self, *args, **kwargs):
"""Pipeline for singular exchange, select a pair, choose exchange direction, apply relevant strategy"""
self.counter += 1
# select random pair
i, j = self._select_pair()
# select random exchange direction
exchange_direction = self._exchange_direction()
self._exchange_strategy(self._agents, i, j, exchange_direction)
if self.counter % (self._max_exchanges / 10) == 0:
self._write_to_file()
def token_exchange_shuffle(self, single_process=True):
"""Exchange tokens `self._max_exchanges` times"""
if not single_process:
raise ValueError("Currently parallel processing is not supported")
else:
for _ in range(self._max_exchanges):
self._shuffle_and_exchange(self)
def get_token_dist(self):
return [(key, value) for key, value in sorted(self._agents.items())]
The agent exchange strategy in turn is defined as below:
def simple_exchange_strategy(agent_dict, i, j, exchange):
"""Simple exchange strategy that will cause exchange of token between agent_i and agent_j
for given exchange type
"""
if exchange > 0:
if agent_dict[j] > 0:
agent_dict[j] -= 1
agent_dict[i] += 1
elif exchange < 0:
if agent_dict[i] > 0:
agent_dict[j] += 1
agent_dict[i] -= 1
The initial parameters given to the class were:
total_agents = 1000
agents = {idx: 50 for idx in range(total_agents)}
max_exchanges = total_agents * 10000
and I captured distribution of tokens held by agents every 1M exchanges.
Results and analysis
The following snippets are copied from my jupyter notebook:
# get supporting libraries
import matplotlib.pyplot as plt
import json
import pandas as pd
import numpy as np
#import and load generated data
data = []
with open(file='Intermediate_agent_calc_atot-1000_time-20190209-225516', mode='r') as f:
lines = f.readlines()
for line in lines:
data.append(json.loads(line))
def human_format(num):
"""Reformat number to be more human friendly"""
magnitude = 0
while abs(num) >= 1000:
magnitude += 1
num /= 1000.0
return '%.2f%s' % (num, ['', 'K', 'M', 'G', 'T', 'P'][magnitude])
#Let's have a look at mean and standard deviation
for i in range(0, len(data)):
tokens = [token for token in data[i]['agents'].values()]
std = np.std(tokens)
m = np.mean(tokens)
print("mean={}, st_dev={} after: {} exchanges".format(np.round(m, 2), np.round(std, 2), human_format(data[i]['exchanges'])))
mean=50.0, st_dev=31.18 after: 1.00M exchanges
mean=50.0, st_dev=38.19 after: 2.00M exchanges
mean=50.0, st_dev=40.48 after: 3.00M exchanges
mean=50.0, st_dev=42.88 after: 4.00M exchanges
mean=50.0, st_dev=44.64 after: 5.00M exchanges
mean=50.0, st_dev=46.13 after: 6.00M exchanges
mean=50.0, st_dev=46.67 after: 7.00M exchanges
mean=50.0, st_dev=47.51 after: 8.00M exchanges
mean=50.0, st_dev=46.55 after: 9.00M exchanges
mean=50.0, st_dev=45.1 after: 10.00M exchanges
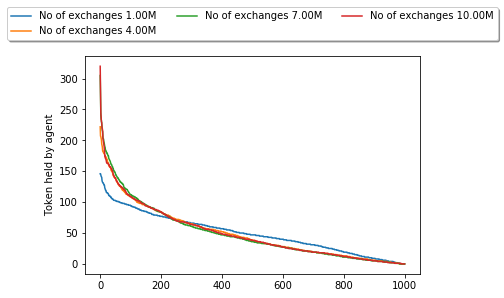
#Let's have a look at few intermediate snapshots of agent distributions up to maximum number of calculated exchanges
fig = plt.figure()
ax = plt.subplot(111)
for i in range(0, len(data), 3):
key_tokens = [(int(key), value) for key, value in sorted(data[i]['agents'].items())]
x, y = zip(*key_tokens)
y = sorted(y, reverse=True)
x = sorted(x)
exchanges = data[i]['exchanges']
_ = plt.plot(x, y, label='No of exchanges %s' % human_format(exchanges))
plt.ylabel('Token held by agent')
ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.25),
ncol=3, fancybox=True, shadow=True)
# Let's have a look probability distribution of agents
# 1. define a function to calculate a probability of getting `x` or less tokens in an array `t` of tokens,
# this helps me see what kind of distribution function my data follows
# 2. Guess the distribution, find its analytical form and plot it alongside the calculated data. From the above plots it looks like the distribution is an exponential distribution.
def EvalCdf(t, x):
"""Cumulative distribution Function that maps from a value `x` to its percentile rank"""
count = 0.0
for value in t:
if value <= x:
count += 1
prob = count / len(t)
return prob
# Picking the last agents `snapshot` after 10M exchenges
y = sorted(y)
probs_y = [EvalCdf(y, x) for x in y]
# analytical form of cumulative probablility distribution function. I did find prefix of `x` by trial and error.
y_calc = [1 - np.exp(-0.020 * x) for x in y]
_ = plt.plot(y, probs_y)
_ = plt.plot(y, y_calc)
_ = plt.axvline(x=50, linestyle='--')
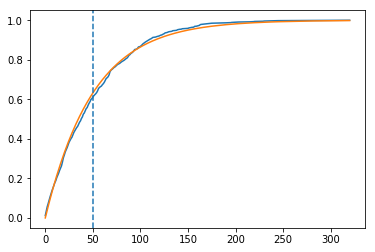
What is the probability of agent having 50 or less tokens?
prob_less_50 = 1 - np.exp(-0.020 * 50)
# Probability of finding an agent of 50 tokens and less?
"P(x <= 50) = %.2f" % prob_less_50
'P(x <= 50) = 0.63'
prob_less_80 = 1 - np.exp(-0.020 * 80)
# Probability of finding an agent of 80 tokens and less?
"P(x <= 80) = %.2f" % prob_less_80
'P(x <= 80) = 0.80'
count_above_80 = sum(1 for key, value in data[9]['agents'].items() if value >= 80)
Lets calculate the number of agents that have 150 and more tokens out of the whole population
print(count_above_80)
215
sum_all_tokens = sum(value for _, value in data[9]['agents'].items())
The sum af all tokens held by all agents - just checking
print(sum_all_tokens)
50000
sum_all_tokens_more_80 = sum(value for _, value in data[9]['agents'].items() if value >= 80)
How many tokens altogether are held by agents that have 80 and more tokens
print(sum_all_tokens_more_80)
25737 <strong>Let's quickly do some simple calculations</strong>
"Percentage of agents that have 80 or more tokens: %.2f %%" % ((count_above_80 / len(data[9]['agents'])) * 100)
'Percentage of agents that have 80 or more tokens: 21.50 %'
"Percentage of tokens held by agents with 80 or more tokens %.2f %%" % ((sum_all_tokens_more_80 / sum_all_tokens) * 100)
'Percentage of tokens held by agents with 80 or more tokens 51.47 %'
Conclusions, few things to ponder about and further work
As one can see simple random exchange of tokens between agents generates an exponential distribution. The first surprising find, by inspecting the standard deviation with increasing number of exchanges, shows that it settles after about 5-6 Million exchanges. Furthermore, what really intrigues me is that around 20% of all agents ended up holding about 50% of all tokens. Finally, about 60% of agents ended up with less than 50 initial tokens.
But how does this relates to anything in the real world? Well if you think about the distribution of wealth, although not completely random it also follows an exponential distribution function with minority of members owning majority of wealth.
According to article “The distribution of household wealth in the UK” in reference [1] “the top 10% hold over 50% of wealth”. The distribution somehow appears to have also a larger area for the top 20% of surveyed population. Nonetheless, further investigation would be required for me to talk about the comparison.
Nonetheless, this is a toy model only serving a purpose of presenting a simple concept of random distribution of stuff and should be taken with a pinch of salt.
What I will investigate in the future is to make different starting conditions, tweak the way we make the exchanges and possibly try to make agents a bit more “sinister” by doing a bit more than simply giving or accepting tokens.
[1] https://www.ifs.org.uk/publications/8239